At Backblaze we have built an extremely cost-effective storage system that enables us to offer a great price on our online backup service. Along the path to building our storage system, we have used time-tested technologies off the shelf, but we have also built in-house technologies ourselves when things weren’t available, or when the price was too high.
We have taken advantage of many open-source projects, and want to do our part in contributing back to the community. Our first foray into open-source was our original Storage Pod design, back in September of 2009.
Today, we are releasing our latest open-source project: Backblaze Reed-Solomon, a Java library for erasure coding.
An erasure code takes a “message,” such as a data file, and makes a longer message in a way that the original can be reconstructed from the longer message even if parts of the longer message have been lost. Reed-Solomon is an erasure code with exactly the properties we needed for file storage, and it is simple and straightforward to implement. It ensures that an entire data element can be recovered even when part or parts of the original stored data element are lost or unavailable.
Download the Open-Source Code
You can find the source code for Backblaze Reed-Solomon on GitHub.
The code is licensed with the MIT License, which means that you can use it in your own projects for free. You can even use it in commercial projects. We’ve put together a video titled: “Reed-Solomon Erasure Coding Overview” to get you started.
Erasure Codes and Storage
Erasure coding is standard practice for systems that store data reliably, and many of them use Reed-Solomon coding.
The RAID system built into Linux uses Reed-Solomon. It has a carefully tuned Reed-Solomon implementation in C that is part of the RAID module. Microsoft Azure uses a similar, but different, erasure coding strategy. We’re not sure exactly what Amazon S3 and Google Cloud Storage use because they haven’t said, but it’s bound to be Reed-Solomon or something similar. Facebook’s new cold storage system also uses Reed-Solomon.
If you want reliable storage that can recover from the loss of parts of the data, then Reed-Solomon is a well-proven technique.
Backblaze Vaults Utilize Erasure Coding
Earlier this year, I wrote about Backblaze Vaults, our new software architecture that allows a file to be stored across multiple Storage Pods, so that the file can be available for download even when some Storage Pods are shut down for maintenance.
To make Backblaze Vaults work, we needed an erasure coding library to compute “parity” and then use it to reconstruct files. When a file is stored in a Vault, it is broken into 17 pieces, all the same size. Then three additional pieces are created that hold parity, resulting in a total of 20 pieces. The original file can then be reconstructed from any 17 of the 20 pieces.
We needed a simple, reliable, and efficient Java library to do Reed-Solomon coding, but didn’t find any. So we built our own. And now we are releasing that code for you to use in your own projects.
Performance
Backblaze Vaults store a vast amount of data and need to be able to ingest it quickly. This means that the Reed-Solomon coding must be fast. When we started designing Vaults, we assumed that we would need to code in C to make things fast. It turned out, though, that modern Java virtual machines are really good, and the just-in-time compiler produces code that runs fast.
Our Java library for Reed-Solomon is as fast as a C implementation, and is much easier to integrate with a software stack written in Java.
A Vault splits data into 17 shards, and has to calculate three parity shards from that, so that’s the configuration we use for performance measurements. Running in a single thread on Storage Pod hardware, our library can process incoming data at 149 megabytes per second. (This test was run on a single processor core, on a Pod with an Intel Xeon E5-1620 v2, clocked at 3.70GHz, on data not already in cache memory.)
Reed-Solomon Encoding Matrix Example
Feel free to skip this section if you aren’t into the math.
We are fortunate that mathematicians have been working on matrix algebra, group theory, and information theory for centuries. Reed and Solomon used this body of knowledge to create a coding system that seems like magic. It can take a message, break it into n pieces, add k “parity” pieces, and then reconstruct the original from n of the (n+k) pieces.
The examples below use a “4+2” coding system, where the original file is broken into four pieces, and then two parity pieces are added. In Backblaze Vaults, we use 17+3 (17 data plus three parity). The math—and the code—works with any numbers as long as you have at least one data shard and don’t have more than 256 shards total. To use Reed-Solomon, you put your data into a matrix. For computer files, each element of the matrix is one byte from the file. The bytes are laid out in a grid to form a matrix. If your data file has “ABCDEFGHIJKLMNOP” in it, you can lay it out like this:
In this example, the four pieces of the file are each four bytes long. Each piece is one row of the matrix. The first one is “ABCD.” The second one is “EFGH.” And so on.
The Reed-Solomon algorithm creates a coding matrix that you multiply with your data matrix to create the coded data. The matrix is set up so that the first four rows of the result are the same as the first four rows of the input. That means that the data is left intact, and all it’s really doing is computing the parity.
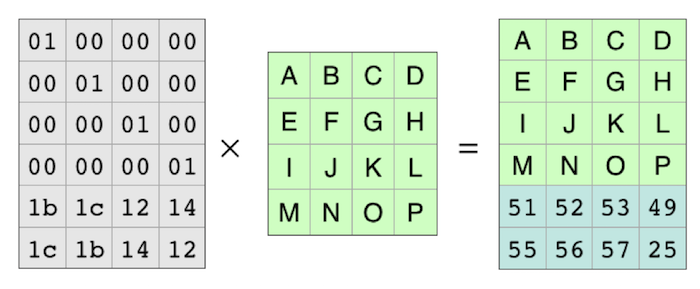
The result is a matrix with two more rows than the original. Those two rows are the parity pieces.
Each row of the coding matrix produces one row of the result. So each row of the coding matrix makes one of the resulting pieces of the file. Because the rows are independent, you can cross out two of the rows and the equation still holds.
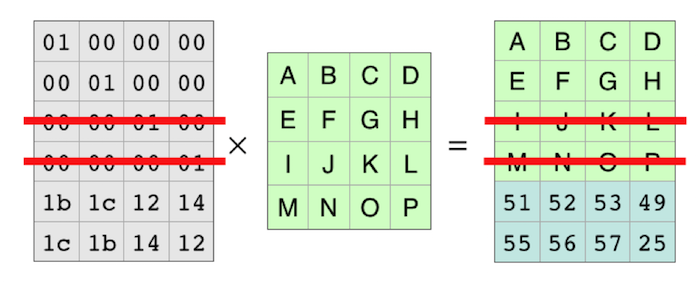
With those rows completely gone, it looks like this:
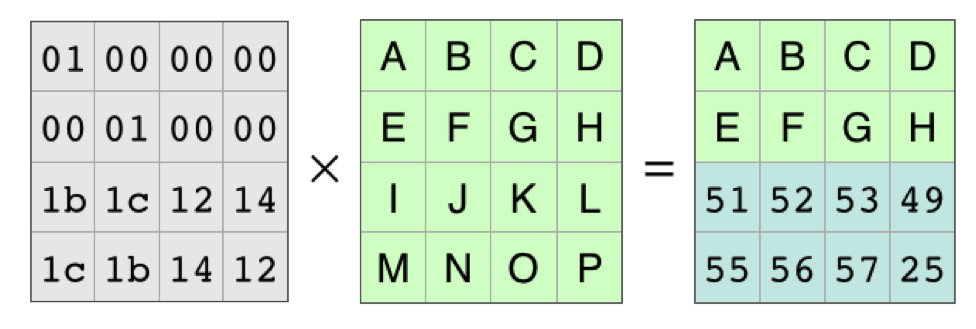
Because of all the work that mathematicians have done over the years, we know the coding matrix, the matrix on the left, is invertible. There is an inverse matrix that, when multiplied by the coding matrix, produces the identity matrix. As in basic algebra, in matrix algebra you can multiply both sides of an equation by the same thing. In this case, we’ll multiply on the left by the identity matrix:
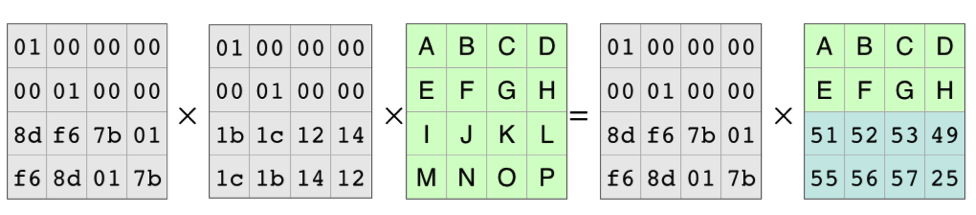The Inverse Matrix and the Coding Matrix Cancel Out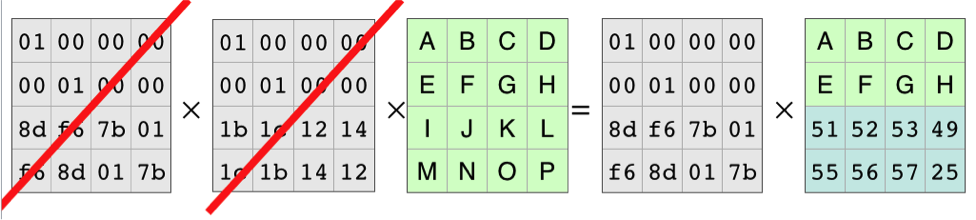
This leaves the equation for reconstructing the original data from the pieces that are available:
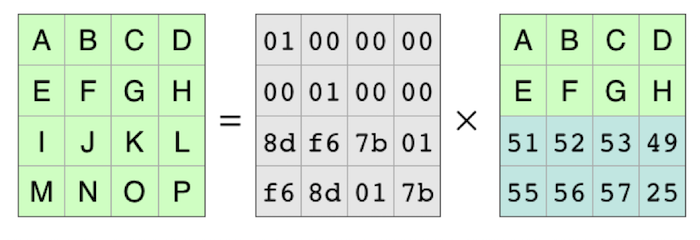
So to make a decoding matrix, the process is to take the original coding matrix, cross out the rows for the missing pieces, and then find the inverse matrix. You can then multiply the inverse matrix and the pieces that are available to reconstruct the original data.
Summary
That was a quick overview of the math. Once you understand the steps, it’s not super complicated. The Java code goes through the same steps outlined above.
There is one small part of the code that does the actual matrix multiplications that has been carefully optimized for speed. The rest of the code does not need to be fast, so we aimed more for simple and clear.
If you need to store or transmit data, and be able to recover it if some is lost, you might want to look at Reed-Solomon coding. Using our code is an easy way to get started.
