Backblaze Durability Calculates at 99.999999999% — And Why It Doesn’t Matter

One of the most often talked about, but least understood, metrics in our industry is the concept of “data durability.” It is often talked about in that nearly everyone quotes some number of nines, and it is least understood in that no one tells you how they actually computed the number or what they actually mean by it.

It strikes us as odd that so much of the world depends on the concept of RAID and Encodings, but the calculations are not standard or agreed upon. Different web calculators allow you to input some variables but not the correct or most important variables. In almost all cases, they obscure the math behind how they spit out their final numbers. There are a few research papers, but hardly a consensus. There just doesn’t seem to be an agreed upon standard calculation of how many “9s” are in the final result. We’d like to change that.

In the same spirit of transparency that leads us to publish our hard drive performance stats, open source our Reed-Solomon Erasure Code, and generally try to share as much of our underlying architecture as practical, we’d like to share our calculations for the durability of data stored with us.

We are doing this for two reasons:

1. We believe that sharing, where practical, furthers innovation in the community.
2. Transparency breeds trust. We’re in the business of asking customers to trust us with their data. It seems reasonable to demonstrate why we’re worthy of your trust.

11 Nines Data Durability for Backblaze B2 Cloud Storage

At the end of the day, the technical answer is “11 nines.” That’s 99.999999999%. Conceptually, if you store 1 million objects in B2 for 10 million years, you would expect to lose 1 file. There’s a higher likelihood of an asteroid destroying Earth within a million years, but that is something we’ll get to at the end of the post.

How to Calculate Data Durability

Amazon’s CTO put forth the X million objects over Y million years metaphor in a blog post. That’s a good way to think about it — customers want to know that their data is safe and secure.

When you send us a file or object, it is actually broken up into 20 pieces (“shards”). The shards overlap so that the original file can be reconstructed from any combination of any 17 of the original 20 pieces. We then store those pieces on different drives that sit in different physical places (we call those 20 drives a “tome”) to minimize the possibility of data loss. When one drive fails, we have processes in place to “rebuild” the data for that drive. So, to lose a file, we have to have four drives fail before we had a chance to rebuild the first one.

The math on calculating all this is extremely complex. Making it even more interesting, we debate internally whether the proper calculation methodology is to use the Poisson distribution (the probability of continuous events occurring) or Binomial (the probability of discrete events). We spent a shocking amount of time debating this and believe that both arguments have merits. Rather than posit one absolute truth, we decided to publish the results of both calculations (spoiler alert: either methodology tells you that your files are safe with Backblaze).

The math is difficult to follow unless you have some facility with advanced statistics. We’ll forgive you if you want to skip the sections entirely, just click here.

Poisson Distribution

When dealing with the probability of X number of events occuring in a fixed period of time, a good place to start is the Poisson distribution.^[1]

For inputs, we use the following assumptions:^[2]

1. The average rebuild time to achieve complete parity for any given B2 object with a failed drive is 6.5 days. A given file uploaded to Backblaze is split into 20 “shards” or pieces. The shards are distributed across multiple drives in a way that any drive can fail and the file is fully recoverable — a file is not lost unless four drives were to fail in a given vault before they could be “rebuilt.” This rebuild is enabled through our Reed-Solomon Erasure Code. Once one drive fails, the other shards are used to “rebuild” the data on the original drive (creating, for all practical purposes, an exact clone of the original drive).

   The rule of thumb we use is that for every 1 TB needed to be rebuilt, one should allow 1 day. So a 12 TB drive would, on average, be rebuilt after 12 days. In practice, that number may vary based on a variety of factors, including, but not limited to, our team attempting to clone the failed drive before starting the rebuild process. Based on whatever else may be happening at a given time, a single failed drive may also not be addressed for one day. (Remember, a single drive failure has a dramatically different implication than a hypothetical third drive failure within a given vault — different situations would call for different operational protocols.) For the purposes of this calculation, and a desire to provide simplicity where possible, we assumed an average of a one day lag time before we start the rebuild.

2. The annualized failure rate of a drive is 0.81%. For the trailing 60 days while we were writing this post, our average drive failure rate was 0.81%. Long time readers of our blog will also note that hard drive failure rates in our environment have fluctuated over time. But we also factor in the availability of data recovery services including, but not limited to, those offered by our friends at DriveSavers. We estimate a 50% likelihood of full (100%) data recovery from a failed drive that’s sent to DriveSavers. That cuts the effective failure rate in half to 0.41%.

For our Poisson calculation, we use this formula:

The values for the variables are:

• Annual average failure rate = 0.0041 per drive per year on average
• Interval or "period" = 156 hours (6.5 days)
• Lambda = ((0.0041 * 20)/((365*24)/156)) =0.00146027397 for every "interval or period"
• e = 2.7182818284
• k = 4 (we want to know the probability of 4 “events” during this 156 hour interval)

Here’s what it looks like:

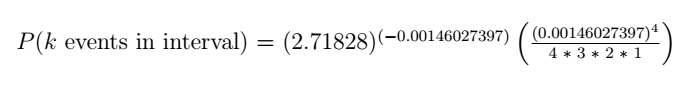
If you’re following along at home, type this into an infinite precision calculator:^[3]

(2.7182818284^(-0.00146027397)) * (((0.00146027397)^4)/(4*3*2*1))

The sub result for 4 simultaneous drive failures in 156 hours = 1.89187284e-13. That means the probability of it NOT happening in 156 hours is (1 – 1.89187284e-13) which equals 0.999999999999810812715 (12 nines).

But there’s a “gotcha.” You actually should calculate the probability of it not happening by considering that there are 56 “156 hour intervals” in a given year. That calculation is:

= (1 - 1.89187284e-13)^56
= (0.999999999999810812715)^56
= 0.99999999999 (11 "nines")

Yes, while this post claims that Backblaze achieves 11 nines worth of durability, at least one of our internal calculations comes out to 12 nines. Why go with 11 and not 12?

1. There are different methodologies to calculate the number, so we are publishing the most conservative result.
2. It doesn’t matter (skip to the end of this post for more on that).

Binomial Distribution

For those interested in getting into the full detail of this calculation, we made a public repository on GitHub. It’s our view on how to calculate the durability of data stored with erasure coding, assuming a failure rate for each shard, and independent failures for each shard.

First, some naming. We will use these names in the calculations:

• S is the total number of shards (data plus parity)
• R is the repair time for a shard in days: how long it takes to replace a shard after it fails
• A is the annual failure rate of one shard
• F is the failure rate of a shard in R days
• P is the probability of a shard failing at least once in R days
• D is the durability of data over R days: not too many shards are lost

With erasure coding, your data remains intact as long as you don’t lose more shards than there are parity shards. If you do lose more, there is no way to recover the data.

One of the assumptions we make is that it takes R days to repair a failed shard. Let’s start with a simpler problem and look at the data durability over a period of R days. For a data loss to happen in this time period, P+1 shards (or more) would have to fail.

We will use A to denote the annual failure rate of individual shards. Over one year, the chances that a shard will fail is evenly distributed over all of the R-day periods in the year. We will use F to denote the failure rate of one shard in an R-day period:

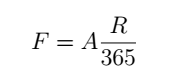
The probability of failure of a single shard in R days is approximately F, when F is small. The exact value, from the Poisson distribution is:

Given the probability of one shard failing, we can use the binomial distribution’s probability mass function to calculate the probability of exactly n of the S shards failing:

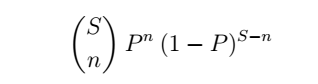
We also lose data if more than n shards fail in the period. To include those, we can sum the above formula for n through S shards, to get the probability of data loss in R days:

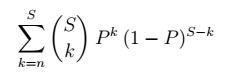
The durability in each period is inverse of that:

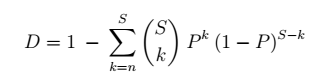
Durability over the full year happens when there’s durability in all of the periods, which is the product of probabilities:

And that’s the answer!

For the full calculation and explanation, including our Python code, please visit the GitHub repo:

https://github.com/Backblaze/erasure-coding-durability/blob/master/calculation.ipynb

We’d Like to Assure You It Doesn’t Matter

For anyone in the data business, durability and reliability are very serious issues. Customers want to store their data and know it’s there to be accessed when it’s needed. Any relevant system in our industry must be designed with a number of protocols in place to insure the safety of our customer’s data.

But at some point, we all start sounding like the guitar player for Spinal Tap. Yes, our nines go to 11. Where is that point? That’s open for debate. But somewhere around the 8th nine we start moving from practical to purely academic.^[4] Why? Because at these probability levels, it’s far more likely that:

• An armed conflict takes out data center(s).
• Earthquakes / floods / pests / or other events known as “Acts of God” destroy multiple data centers.
• There’s a prolonged billing problem and your account data is deleted.

That last one is particularly interesting. Any vendor selling cloud storage relies on billing its customers. If a customer stops paying, after some grace period, the vendor will delete the data to free up space for a paying customer.

Some customers pay by credit card. We don’t have the math behind it, but we believe there’s a greater than 1 in a million chance that the following events could occur:

• You change your credit card provider. The credit card on file is invalid when the vendor tries to bill it.
• Your email service provider thinks billing emails are SPAM. You don’t see the emails coming from your vendor saying there is a problem.
• You do not answer phone calls from numbers you do not recognize; Customer Support is trying to call you from a blocked number; they are trying to leave voicemails but the mailbox is full.

If all those things are true, it’s possible that your data gets deleted simply because the system is operating as designed.

What’s the Point? All Hard Drives Will Fail. Design for Failure.

Durability should NOT be taken lightly. Backblaze, like all the other serious cloud providers, dedicates valuable time and resources to continuously improving durability. As shown above we have 11 nines of durability. More importantly, we continually invest in our systems, processes, and people to make improvements.

Any vendor that takes the obligation to protect customer data seriously is deep into “designing for failure.” That requires building fault tolerant systems and processes that help mitigate the impact of failure scenarios. All hard drives will fail. That is a fact. So the question really is “how have you designed your system so it mitigates failures of any given piece?”

Backblaze’s architecture uses erasure code to reliably get any given file stored in multiple physical locations (mitigating against specific types of failures like a faulty power strip). Backblaze’s business model is profitable and self-sustaining and provides us with the resources and wherewithal to make the right decisions. We also make the decision to do things like publish our hard drive failure rates, our cost structure, and this post. We also have a number of ridiculously intelligent, hard working people dedicated towards improving our systems. Why? Because the obligation around protecting your data goes far beyond the academic calculation of “durability” as defined by hard drive failure rates.

Eleven years in and counting, with over 600 petabytes of data stored from customers across 160 countries, and well over 30 billion files restored, we confidently state that our system has scaled successfully and is reliable. The numbers bear it out and the experiences of our customers prove it.

And that’s the bottom line for data durability.

[1] One aspect of the Poisson distribution is that it assumes that the probability of failure is constant over time. Hard drives, in Backblaze’s environment, exhibit a “bathtub curve” for failures (higher likelihood of failure when they are first turned on and at the forecasted end of usable life). While we ran various internal models to account for that, it didn’t have a practical effect on the calculation. In addition, there’s some debate to be had about what the appropriate model is — at Backblaze, hard drives are thoroughly tested before putting them into our production system (affecting the theoretical extreme front end of the bathtub curve). Given all that, for the sake of a semblance of simplicity, we present a straightforward Poisson calculation.

[2] This is an area where we should emphasize the conceptual nature of this exercise. System design and reality can diverge.

[3] The complexity will break most standard calculators.

[4] Previously, Backblaze published its durability to be 8 nines. At the time, it reflected what we knew about drive failure rates and recovery times. Today, the failure rates are favorable. In addition, we’ve worked on and continue to innovate solutions around speeding up drive replacement time.